クォータニオンライブラリの実装がてらクォータニオンのLWでの回転(B->P->Hの順に回転)への分解(※1)やCCD法(※2)などを考えていたのだが、単体事象の解析は先日のような行列処理系でできるのだが、複合的な問題を考える場合は行列とは別に配列や構造体の実装が必要になる. 今ある言語を拡張するかあるいは物理シミュレーション等の検証用に実数系の行列やクォータニオンを統一的に扱える言語を新しく起こす方が楽か.

取りあえずは現状の3DプロッタコアなどをベースにC++でDOSのプログラムっぽく安直に検証するフレームワークを作ってみて考えるのも良いかもしれない、自分は頭が悪い為OpenGLの管理とロジック部分が混在してしまうと効率的にアルゴリズムを考えられなくなる、何よりメインの事象(ここでは計算ロジック)を考えながら関係の無いコード(3Dの表示やバッファのコピー、行列のリテラル表記等)をいじっていると血圧が上がって仕方無い、何とも馬鹿馬鹿しい気がして正直関係無いコードは1行たりとも書きたくない. まぁ無能ほど道具に頼ろうとするというヤツなのだが(苦笑)

※1) しかし幾らクォータニオンを使っても内部形式が行列表現では無くオイラー角である時点で駄目だなぁ、という所もアリにて. 誤魔化しはできるがジンバルロック時に解なしになるなど根本的な問題は残ったまま、モーション系のプラグインがオイラー角を参照してモーションを決定している事を考えると過去の互換性からはどうにもならないのだろうけど、もう少しどうにかならないものかなぁ:-<＞LW

※2) CCD法はInverseKinematicsを計算する最も簡単な方法の一つ、IKチェーンの先端からゴールへの方向へ回転を行う事を親アイテム方向に繰り返す、IKの根元まで来たらまた先端に戻り適当な回数反復する事で解に漸近化する.

電卓がてら特殊関数ライブラリを実装、まぁ大学時代ならともかく今の自分には余り必要無いものだけど;-)

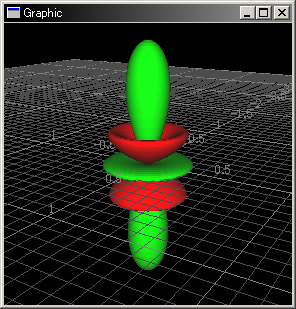
その中では今でも使う可能性がありそうなLegendre倍関数のテストでよくある球面調和関数のプロットを作ってみた.

こんなカンジ (画像は l=4,m=0の実部) 係数の変更や虚部or複素共役の2乗プロット等、自分でやってみたい人はこちら DLしたアーカイブ内のsph.txtをmcl.exeにドラッグすると上の画面が表示されます. l,mの値を変えたい場合は sph.txtの41行目を変更の事、値は l>=0, abs(m)<=lで設定、lを増やすにつれ(所謂)周波数が増加、m=0で軸方向に広がっている関数がmの絶対値を増やすにつれ赤道方向に広がるのが確認できます.

なおmcl.exeは簡易matlab+R(orS)言語もしくはAPLモドキの自前の処理系(電卓代わり)で全ての演算が2次元の表(行列)に展開されるカンジ(笑)

---------------

特殊関数の実装で少々難儀したのがGaussの誤差関数erfの逆関数の実装、他は文献などにあるものを改造して使ったのだが、これだけは無かったので自前で考える事に、という事で実装はこんな具合、マクローリン展開の結果であたりを付けNewton法で漸近化する手法、前提としてある程度正確な値を返すerfが実装されている事.

double inverf(double x){
    if(x < -1 || 1 < x) return NAN_DOUBLE;

    double r;
    r=(1/2.*x + 1/24.*PI*pow(x,3) + 7/960.*pow(PI,2)*pow(x,5) + 127/80640.*pow(PI,3)*pow(x,7));
    r*=sqrt(PI);

    /* Newton法で近似(平均30回程度で収束) */
    int i;
    double prev=r;
    for(i=0;i < 100;++i){
        r-=(erf(r)-x) / (2.0/sqrt(PI)*exp(-r*r));
        if(prev==r) break;
        prev=r;;
    }

    return r;
}

GNUPlotに実装されているのは知っているのだけど、それを参考にしてしまうとGPLに引っかかるので自前で、取り合えず上のコードの著作権などは放棄されていると考えてください(ま、そんなに大層なものでは無いですが)

なお 2.0/sqrt(PI)*exp(-r*r)はerfの導関数で、ソースにあるNAN_DOUBLEはdouble型のNAN値の定義で別途自前での定義が必要. erfも実装によっては反復を伴う為Newton法の部分は結構コスト高、気になる場合は上の関数をベースに-1〜1区間でChebyshev多項式などで近似する等適当に.

---------------

とまーそんな具合、先日のしかとの影響で頭の中でヨーデルが延々流れててどうしようも無いです、壁に向かって何も考えずただまっすぐ歩きたい気分、そして頭をガッツンガッツンぶつけたら幸せになれそうな予感(笑)

次はちょっと脇道に逸れて楕円曲線上での加算問題に手をつけようかと思ってます:-P

しかと&しかとが動くページ

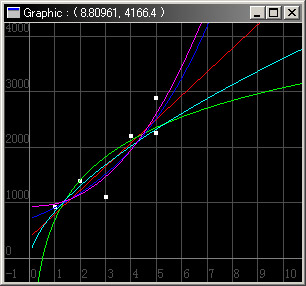
最高ですよ、ええ、素晴らしすぎます。

---------------

久しぶりの線形(単)回帰分析、正確に言うと紫だけは多項式だけど、というか大学以来余り使いませんねー、まぁプログラマというお仕事はどちらかというと計算のメソッドを扱う事はあってもデータ自体を扱う事は稀なんですが、ちなみに大学時代は最小二乗法の方程式解法しか実験のインストラクターが教えてくれなかったのでえらい苦労した記憶があります (というか余りに面倒で殺意すら感じました) まともな解法を知ったのはそれから暫くたってからの事sigh

まーだからどうしたって程度の話ですが、電卓のエンジンテストです(笑)

というかね、、、エンジンよりもインターフェイスの設計の方が難しい、所詮電卓、複雑になったりくどくなったら終わりだし、出来る事に欲を出すと(インターフェイス的に)計算プログラムには遠く及ばないし、でも余り安直が過ぎると市販の関数電卓のプログラム可能版にすら劣るし.

というか個人的にはBASIC処理系も電卓の一種なんですが(Excelに追いやられた感はあって流行りませんけど、計算式など検証するには便利なんですけどね:-)

---------------

統計の勉強、進めるにつれてなんかこれの初等版(正規分布の検定程度まで)は高校で教えろよって気になってきます、何か内容的に統計の読み方とか簡単な予測とか一般教養な気がする、、、断片的な情報集めて勉強するのって苦労するんだから、ブツブツ、みたいな.

まぁ実際は電卓なり表計算ソフトが無いと計算が多くて学校で教え辛いって背景もあるのかもしれないけど、だからってこんな当たり前に近い話はちゃんと教育課程に入れといて欲しい所です. 時代も変わっているんだし:-<

何となしに統計の勉強始めました、取り合えず初等的な内容 (正規分布とそれに付随する分布の検定や推定位まで) は押さえようかと思ってます. というか気晴らしに簡単な電卓でも作ろうかと思い昔愛用していたHP200LXのMath,Solver,Stat程度のものと考えたのだが、Stat(それ自体はどちらかというと回帰分析用)を作っている時に、背景にある統計の話を余り知らない事に気付いたので.

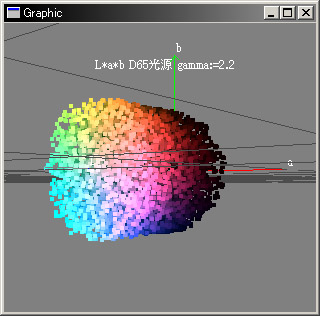
現在入門書を読み漁りながらExcelなどにある分布・逆引きの関数を実装していたり、延々Numerical Recipie in C(*1)を読んでいたりとそんなカンジ. 結構楽しい.

ついでにSolverも単純にNewton法では初期値がシビアなんで割線法 (Newton法と同じ特性だが初期状態等を工夫してやると一部の形の関数でNewton法より良い収束を出してくれる) やら2分法での区間推定をあーでもないこーでもないといじってみたり、特異点を避ける為に条件を色々ずらすようにしてみたり、論文とかアカデミックな話よりもエンジニア的な工夫の方が安定性(あくまで浮動小数という有限精度での想定だけど)に貢献している辺りはいとおかし (と言ってだからアカデミック系は駄目なんだみたいな話に飛びつかないように＞誰? あくまで両方のアプローチでより工夫できるやねとかそういう話.

つまりは、現実逃避(駄目じゃん、いやまー仕事の方は完全に「いかんね」ってカンジなもんで:-<

*1) (古典だけど)至高の一冊、どうでも良いがこの本、大学時代(購入当初)よりよっぽど今の方が役に立っている、、、如何に大学時代遊びほうけていたかという所かorz

---------------

年末に書いていた汎用スクリプトの方はプリミティブをObjectにするコアを作った後停滞中、Utilとして見るなら汎用的なオブジェクトとして定義するよりも組み込みオブジェクトは別扱いの方が機能として便利なものは組み込み易いなぁトカ、シリアライズ入れる場合関数とかどーっすっべや(妥当なのは名前のみ参照だが、First Class Objectとして扱っているので別段定義名が関数にあるワケで無し、あるいはクロージャとかまで考えるとどうするか...:-<)

現在当初の予定(3ヶ月程でサックリ完了)を半年程ズレ込んでいる事になる、、、まぁ当初の想定とはだいぶ言語規模が大きくなっているし、言語を作るの自体もそれはそれで見えてくるものがあるので決して無駄では無いと思うけど、その状態にならないと気付かないのは余り物分かりが良いとは言えないわな:-<

ちなみに先月書いたスクリプトはアルゴリズムの検証や雑用等500行程度、それに対して現在使用中のコアは5万行程度、やはり余り賢いやりかたとは言えないかも:-)

---------------

実写版ゲゲゲの鬼太郎だそうな、、、いや原作は好きなんだけど、サイトに上がってるPVとかある意味呆然、というかこういうビジュアルって元々漫画での想定だから実写にすると違和感が激しい、最近だとアニメのコスプレとかの痛い人を連想してしまって更にキモく感じるし、いっその事実写に合わせたデザインのリメイクした方が遥かに良い気がするんだけど、向こうの映画だとX-MENとか上手くやってた気がする、、、 そういえば一時期噂のあったドラゴンボールの実写版はどうなったんだろう?

---------------

なんとなく文章ばかりでは寂しいのでL*a*b*の3Dプロット(D65光源, gamma=2.2を想定)

最近3Dでの点プロットが空間データのおおまかな把握に非常に便利だと気付く、まぁ正確な分析は輪切りにするけど、ざっくりと把握する場合に拡大すると中の様子まで分かるので(見た目はともかく)結構いーかんじ.

しかし変換式は完成したもののこれってモニタが完全にキャリブレーションされた状態で色温度まで含めデータが揃っていない限り、色の比較程度にしか使えないかも(まぁお前のイメージが貧困なんだって話もアリだがX-<