| 【雑記】 |
| 2009/11/28 |
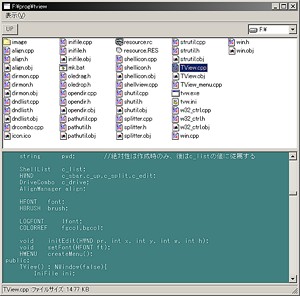
| 諸事情からここ数日PHPをいじっていたが、テキストファイルが多くなるといちいちダブルクリックで開いてファイルを探すのにうんざりしてきたので簡単な内容とファイルリストの同時表示可能なビューアを作る事にする. 無論こんなものは探せば幾つかありそうなのだが、たまたま見つけたものはスクリーンショットが好みで無かったり、ベクター辺りからそれっぽいソフトをダウンロードしてはいちいち試すのも邪魔臭かったので. まぁそれ以外には数日前にC++のOLEのドラッグ&ドロップのルーチンを書き直していたのでそれの追加テストとしても丁度良いかという所. んでおよそ2日弱でこんな↓具合 読み込みはまだ別スレッドにはしていないが、一応リストビューの個所はファイルのコピーやドラッグ&ドロップ、文字コード自動判別など一通り全ての機能が動作する. これで今回起こしたメインのアプリケーション部のコードは1000行程度、非常に面白いと感じたのは、今回のものはC++ & Win32で書いているのだが、以前C# ( .NET2.0 WinForms) で書いた似たような (シェル系の) スタイルのアプリ (グラフィックビューア) も大体同じようなコード量&構造の複雑さになっている事. 無論これはフェアな言い方では無くWin32版の方はそれ以外に自分が普段使っている自前ライブラリ (Windowの汎用クラス基底や文字列,パス処理,OLE処理に標準で用意されていないスプリッタなどのコントロールや自動レイアウト等) などを必要に応じて追加している為、今回のソフトに流用しているライブラリ部分はおよそプラス4000行程度になる ;-) まぁだが所詮は言語に依らずライブラリの有無のみで見られる差異のみで、プログラムの構造の記述という点での複雑さは化石同然(笑)のC++ & Win32でも、先進的な筈のC#でも似たような分量になるのはある意味では滑稽かもなぁなどと思ってみたり. 以前 flex SDKである程度の規模のGUIを作った時も、余りコード量は変わらんなぁ (常にクラス、メソッド主体なので横にはC++より長くなるが(笑)) と思ったのだが、まぁ現実はそんなものかもしれないなど苦笑してみたり ;-) # まー実際には自前で安定したライブラリを作れるかどうかのリスク的な問題や実際の可否、人員追加の場合の同化コストなど考えると一概に一般的な開発論に落とし込めるとも言い難いワケではある (逆に自前ライブラリを擁護するなら、全ての部分で不明な個所が無いコードの集合体としてソフトを組める所は品質保証の観点から非常に大きいとも言えるので一長一短ではある) 一方でこういう事があるとコンピュータ業界に蔓延する技術方法論傾倒主義は結局どれだけの意味があるのかなぁ?など改めて考えさせられる部分も有り.
# 、、、単にPHPからの逃避だろうって? それは言うな(笑)
|
| 2009/11/22 演算子のオーバーロードは恐い. |
| 行列言語をいじっていて1000x1000の行列の乗算を試すと71secもかかっていた、これはイカンという事で高速化を試みる. 元々のデータ型がdouble x 2の複素数型を基にしている為、これを実数に特化した処理を挟む事で実数版については15sec、更にキャッシュ効率を考えて (メモリは余計に食うが) 転置構造を用意してアクセスを工夫する事で3sec程度まで、この差20倍(笑) ただ複素数版は同様の操作をしても速度の向上が見られなかった為、改めて確認すると標準ライブラリの複素数の乗算が重い模様、長いリストの一部なのでアセンブラコードでは確認していないが3重ループの内部で、関数自体の処理が重いのか、インライン展開されず関数呼び出しになっているオーバーヘッドかといった所、誤差なども特に気にする必要の無い性質の演算なので、自前で乗算を展開してやる事でこちらも7sec程度まで、およそ10倍, まー効率化云々の結果はともかく、時に演算子のオーバーロードは見えない所で意外なオーバーヘッドになるなぁと改めて痛感、まーそんなカンジ. 標準ライブラリの組み込みの乗算が遅い事が判明したので、自前の行列関数の複素数版 (LU分解, 逆行列, 行列のランク計算, べき乗の展開等、比較的シンプルなもの、流石に非対称行列の固有値問題とかは虚数域まで含めると自分で組むのはきついのでLAPACK頼み) の個所を1日がかりで見直し、総じて10倍程度の向上は見られた. それ以外にはLAPACKの特異値分解のルーチンと自前のSVD処理結果を比べて検算していたりとまー色々. # 幾らPCが速くなっても3重以上のループはまだ安易に扱うと覿面に重くなるのはペイントソフトの開発で痛感していたのだけど、まーやっぱそんなカンジですねぇ、みたいな. 一時期 (JDK1.1頃だったか) Javaで3Dレンダラを作るプロジェクトが幾つか発生したが、結局その全てが消えて無くなったのは、まだその辺の反復処理の大きく影響するような処理では脳天気にVMとGCの性能にお任せとはいかなかったのかなぁなどと思ってみたり. いや、マジにJavaのGUIライブラリとか.NETのライブラリ構造とか、最近ではFlashのライブラリ構成などを見ていると、これを設計した人ってまともなアプリケーション(※1)書いた事あるのかなぁ?なんて思ってしまう部分もあるのだが、宣伝文句とは裏腹に相変わらずある規模以上のGUIソフトは作るのが難しく実質問題は解決されていないのでは?やっぱIT業界ってオオカミ少年(※2)やマッチポンプ的側面を持っているのかなといった疑念を感じるこの頃だったり ;-) ※1) ここでのアプリケーションというのは、その中にがっつり入り込んで一連のワークフロー全てを閉じた形で提供するソフトの事、ね. 単機能のソフトでは無くて :-P ※1') まぁ何でも1人でできるものじゃないという話はありそうだが、もし (あくまで仮に、だが) 家の一つも満足に建てた事が無い人が作り上げた 「効率的な家の建て方」 なんてガラクタ以外の何物でも無いよーな気もしたり、まぁ余り他者を侮るのは慢心や盲目,停滞にも繋がるので程々にしておくべきで (実際言っていて余り気持ちの良いものでも無いし) 己自身が最大の愚か者である事を忘れてはいけない、とは常に自戒する所ではあるのだが :-< ※2) 実は必要なのは狼男を撃ち殺す銀の弾丸では無くオオカミ少年を撃ち殺す弾丸じゃなかろーか、みたいなそんな言葉遊び :-P
|
| 2009/11/16 あ、、、繋がった(笑) |
| ここ数日は数学の勉強という事で先日書いた特異値分解の模式モデルを色々いじったり (複素数ベクトルの幾何的な意味って何?(涙)) 行列の対角化による関数計算などの話や、幾つかの証明の過程などを追っていたのだが、何か自分の中で「行列の持つ意味」みたいなもののイメージがほぼ繋がったようなカンジ、正方行列についてはある程度掴んでいたけど、特異値分解などを使えば任意の行列を解析できる事や、その勉強に関連して読んでいた直交基底の話と関連するnull/image空間の基底などが、今まで若干モヤモヤしていたものを完全(?)にクリアにしてくれた模様で、行列が明確に頭の中でイメージとして「見える」具合で、何か頭がスッキリしてキモチイイ(笑) 改めて画像の解析系のトピックをまとめた本など読んでみると、いままで漠然としてた部分が凄く良く分かる、例えばよくある顔認識で固有顔を作るような (固有空間法というらしい) なんて、以前はそういうものなのかなーなんて漠然と眺めてた個所が「なーんだ、当たり前じゃーん」みたいなカンジだったり、フーリエ変換や多項式近似の条件になっている関数直交基底についても「そりゃそーなるでしょ」みたいな具合にスルスル頭に入ってくる、多分ドラえもんのマンガでほんやくコンニャクで本を読むシーンで、「おお、分かるぞ」みたいなシーンがあった気がするがこういう気分だったのかなーなんて思ってみたり. まーだからどうだってワケでもなく、せいぜいようやく行列もベクトルと同様に日常的に使える所まで来たかなーという程度の話なのですが、、、ま、スタート地点から出遅れているのでこの辺はもっと頑張りましょうという具合で(苦笑) いや、だからテンション上がってスゴクキモチイイみたいなおチャクラ全開悟りでGO!!(というマンガがあるらしい、実物は知らん(笑)) みたいな、何か妙な所が微妙に開眼した気分ですよ、スーパーサイヤ人全開!!みたいな (で調子に乗っているとフリーザにやられるんだっけ? 余り詳しくないので細かいツッコミ禁止で(笑)) ええ ;-) # いやマジに世界の見え方がもう一つ増えたようなカンジになんか非常に視点がスッキリしているのだよねぇ、マジ妙なトリップ入っちゃってるんじゃないか?みたいにちょっと不安になる位(苦笑)
|
| 2009/11/11 |
| 少し間が空きましたが一応まー生きてます、というカンジで. ペイントソフトもインタプリタも大枠は仕上がっているので、まだ全然完成とは言い難いものの、チマチマとした修正以外にはそもそもそれが対象とするモノをPC上で実現するとは何ぞ也、みたいな. 機能を揃えるだけなら既存のものに追従すりゃ良いので楽なのですが、そろそろそうも言ってられなくなってきてるなーというかまーそんなカンジでぼちぼちです. --------------- 暇をみては大学時代に積み残した数学の勉強、基本的な流れは
の繰り返しといった具合(苦笑) 今の所線形代数で行列の持つ写像や固有ベクトルの意味は掴めたけどまだイマイチ特異値周りが理解できてない. M=P.P~ ( .は行列の乗算、~はHermite共役の演算子) について0では無い固有値は共通(それ以外は退化次元)である事は証明可能、それぞれ対称行列であるので対応する固有ベクトルは直交基底を張る. M=U.Λ.U~ U,Vの よってPは δ=sqrt(Λ)をPの特異値と呼び、U+Vでの変換にある程度歪みの項が含まれるので、固有値/固有ベクトル程正確では無いがPの写像の指標を与える、また固有値と違い任意の行列に適用可能&コンピュータでの計算(SVD)も安定. という事で良いのだろうか? うーん、まだUとVの幾何的な関係とかが掴みきれて無いのだよねぇ、ある程度条件は共有しているので完全に幾何的に無関係な直交基底というワケでは無さそうな気がするし、SVDの説明によるとPのnull/Ker基底やrange/Im基底と関連しているらしーのだけど、式としてはともかくイメージとしてまだ今一つ掴みきれていない :-< それ以外には正方行列の U.sqrt(Λ).inv(U) による平方根や指数関数 (実際には数値的に安定なSchur分解などを使う) など、写像の意味からすると確かにその通りだなーとかまー色々. まだ漠然とはしているのだけど、何か掴みかけているような気がするのでもう少し頑張ってみようと思う. 、、、まー大学時代ちゃんと勉強していればこんな間抜けな事にはなってないのですがorz 2009/11/12追記)
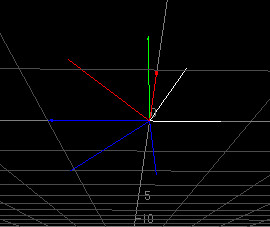
特異行列 [1,1,1][2,2,2][3,3,3]の写像空間のプロット、白が固有ベクトル軸、青が退化軸(null/kernel)空間で赤(固有値の白と重なっている)が写像(range/image)空間、ちなみに青と2本の赤と重なっていない白は同一平面を形成、U,Vはそれぞれ直交基底 (P.P~,P~.Pは対称行列より得られる固有値は実数であり固有ベクトルは互いに直交する) だから得られるKer/Im基底も固有ベクトル表現とは違って直交基底の形で得られるワケね、成程成程、、、ってまーこれだけ出しても自分しか分かりませんが(笑) 、、、しかし、改めて色々なシミュレーション結果を応用する事を考えると別にOpenGL固有ってワケじゃなく従来の学問なんかでも一般的なのは右ベクトル表記なワケで、DirectXの左ベクトル表記って限りなく有り得んよなーやっぱり、何かOpenGLとの非互換戦略だけのマーケット論的なすげー浅はかな思惑だけでやっちゃった的な気が(--;;
|
過去の雑記
2009年 7月〜10月の雑記はありません.
2009年 6月
2009年 5月
2009年 4月
2009年 3月
2009年 2月
2009年 1月
2008年 12月
2008年 11月
2008年 10月
2008年 9月
2008年 8月
2008年 7月
2008年 6月
2008年 5月
2008年 4月
2008年 3月
2008年 2月
2008年 1月
2007年 8月〜12月
2007年 7月
2007年 6月
2007年 5月
2007年 4月の雑記はありません.
2007年 3月
2007年 2月
2007年 1月
2006年 12月
2006年 11月
2006年 10月
2006年 4月〜9月の雑記はありません.
2006年 3月
2006年 2月
2006年 1月
2005年 12月
2005年 11月
2005年 10月
2005年 9月
2005年 8月
2005年 7月
2005年 6月
2005年 5月
2005年 4月
2005年 3月
2005年 2月
2005年 1月
2004年度